MIT OpenCourseWare
MIT 8.04 Quantum Physics I, Spring 2013
View the complete course: http://ocw.mit.edu/8-04S13
Instructor: Allan Adams
In this lecture, Prof. Adams discusses the basic principles of quantum computing. No-cloning theorem and Deutsch-Jozsa algorithm are introduced. The last part of the lecture is devoted to the EPR experiment and Bell’s inequality.
License: Creative Commons BY-NC-SA
More information at http://ocw.mit.edu/terms
More courses at http://ocw.mit.edu
Source
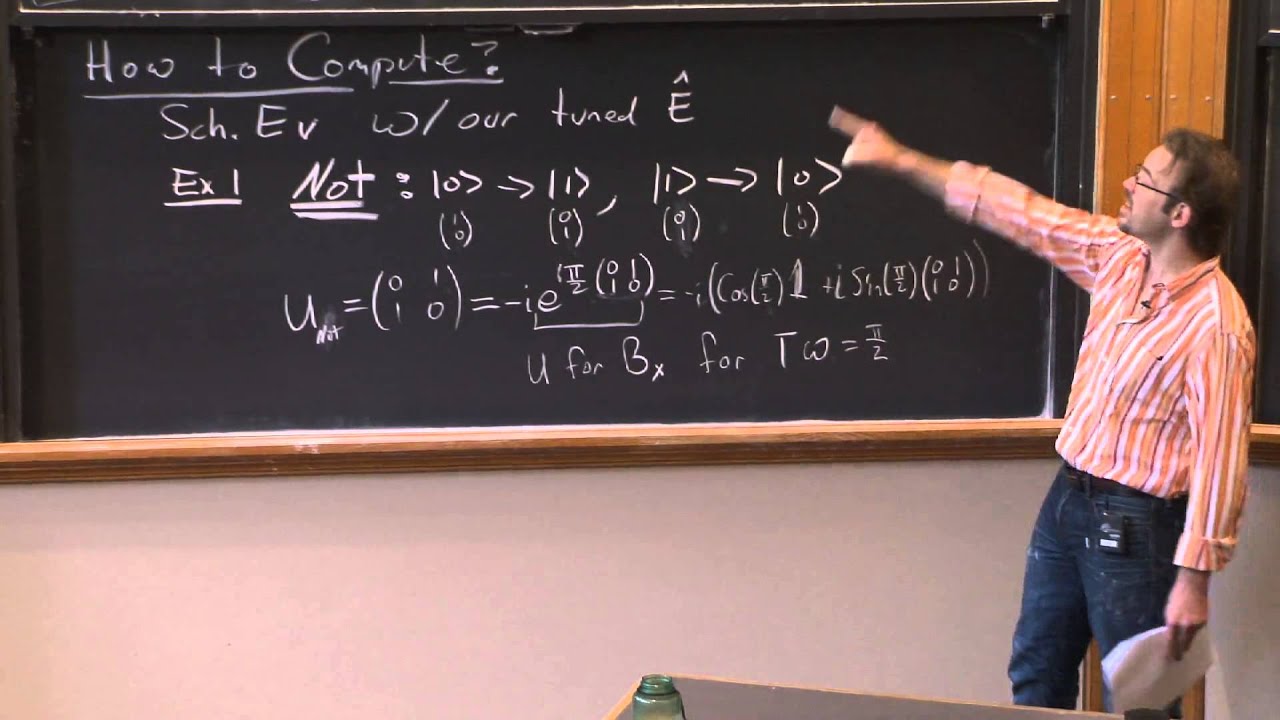



Excellent lecture, but what about self-error correction or verification algorithm? The Deutsch-Josza algorithm was indeed smart.
Classical computers are electronic, quantum computers will be photonic.
Watch it on 0.5 speed lol
Quantum mechanics proves that if we do the EPR experiment repeatedly and build up statistics what we will find is an explicit violation of the Bell's inequality. This is a conclusive empirical proof that there are no classical definite configurations underlying the probability of quantum mechanics
"Quantum physics is the operating system and classical mechanics is the simulation running"
Muy ouija board is missing all this..wow!!!!!
Brilliant teacher! I really enjoy these lectures a lot!
can only talk in jargon at hyper speed
I too wish to thank MIT and Dr. Adams for their hard work and in providing the hoi polloi with the chance to learn this. However, I am also watching Barton Zweibach's version of this course (PHYS 8.04), and the approach is much "simpler" (?) with Zweibach. I wonder if anyone can shed light on the two different approaches, why a change was made from Adams's 2003 version to Zweibach's 2006 version.
@1:21:19 why should be hidden variables be randomly distributed??
In my opinion this is very crucial in establishing inherent randomness, but is simply mentioned but not explained fully.
This was very good, I am still hung up on a lot of the details of the bell inequality. But this has been a nice drop in the bucket of understanding quantum physics.
so will posting here Change MyLife?. am I entangled ? and in what way??
any tips to understand the english??
how we understand the quick english??
Biggest quantum computer is 70+
Lol! He says around 26:30 that we should be very skeptical of philosophy in a physics classroom and then cites our "moral states". good lecture. But I wish there were more philosophy in the class. I believe the conceptual story makes it far easier to internalize/memorize and keep up with.
At 33:23 why can’t you write a separable state (|0> +i |1>) (|0> – i |1>)? Does the ordering of the vectors matter?
Im so confused. I'm trying to understand quantum mechanics for a school project about teleportation. I'm trying to understand how the 4 Bell states come to be. If we have two particles that can be either up or down, then, looking at both at the same time, they could be either both up/ down or one of them is up and one is down.
The 4 Bell states are
sqrt(1/2)*(up up + down down)
sqrt(1/2)*(up up – down down)
sqrt(1/2)*(up down -down up)
sqrt(1/2)*(up down+down up)
I don't know much about this topic so sorry if this question is dumb. I am just stuck trying to imagine the 4 states. What difference does the minus make? They are still either up and up or down and down regardless of the minus or plus right? But what is the difference between the states?
37:00 qcomputing operations
thank allan and mit. perhaps in future prof. could explain the formation of laser using this qm approach.
Awesome just awesome
Wow. I cant understand alot. I guess i need to build up my knowledge elsewhere..
great lectures, in that they make me what to do the problems sets, or attempt, fail, cheat and check solutions. Learn a lot that way, especially all the "naive" information, or assumed knowledge that we have to catch up on to put it all together.
I am about to do EPR this week on campus in Australia this week.
Al, did you fudge "Bell's" a bit? LOVE that you gave us an actually 'inequality' that is violated, they don't do that in our McIntyre textbook (also thanks to MIT for the awsome Linear Algebra recap, text is very heavy on matrix interpretations)
Joining the last bit of first lecture to last bit of the last lecture.
End of 1st lecture you show us in set theory, the inequality reduces number of elements must be greater than or equal to zero, and promise QM can violate. Last lecture you 'play' with probabilities instead, but like set elements, these too can not be negative.
Last lecture, you could have choosen (up@zero, down@2*theta) + (down @2*theta, up@theta) >= (up@zero, down@theta). This statement is true, giving the probabilities (theta^2) + (theta^2)/4 >= (theta^2)/4
Of course, any configuration, just one example is enough to violate a "truth", but not quite the "slam-dunk" that I projected you were claiming (maybe you weren't) OR I got it wrong.
The angles zero @ vertical ('z'), then (2/3)*pi and (4/3)*pi (Mercedes logo) fits the above relation, and used in the textbook, but not with probabilities, but all possible info encoded in each particle such that particles have 100% correlation when measured in the same axis. QM predicts spin up/down pairs %50, but the pre-set variable must come through at greater than %55 up/down pairs. Textbook an exact proof in set theory probability, but less spectacular and impressive than the lecture.
In my opinion, probability is a an aesthetic problem in physics. It can't be represented by a fraction in space-time cause there is the entanglement, which is represented by imaginaries numbers in equations, and to understand more about this, it necessary comprehend about more about the lowest state of energy, quantum vacuum state.
—————
Professor Adams, It will be honour to meet you someday.
I have so many questions.
The derivation of Bell's Inequality goes through if 1) the presumptive hidden variable is static (not time varying) or 2) if the presumptive hidden variable is time varying but both particles age according to a common master clock that pervades the cosmos everywhere and everywhen. Under those simplifying assumptions, the derivation of Bell's Inequality is mathematically sound.
But if you posit a time-varying hidden variable and you allow that each particle ages at its own idiosyncratic rate (e.g. because there are gravitational gradients present in the cosmos), then the step where Bell cancels out the two halves is in trouble. Mathematically, there remains a residual non-zero "beat frequency" and the hidden variable does not vanish from the bottom line.
That is, the not-so-hidden variable is time itself. There is no universal master clock, and the two particles do not age in perfect phase-locked frequency. Or to say it another way, the two functions are not perfect mirror images of each other and therefore do not cancel each other out.