4.3 Reference Frames

20 thoughts on “4.3 Reference Frames”

1. anyone clear my doubt please

   What if the net force on some particle is zero and we choose that particle itself as the reference frame or frame moving uniformly relative to the particle. whether we can call that frame an inertial frame of reference?

2. Damn, Im only sixteen😂

3. Sir which book you have preferred for this

4. Fuck my damn school

5. It was clearly explained thanks

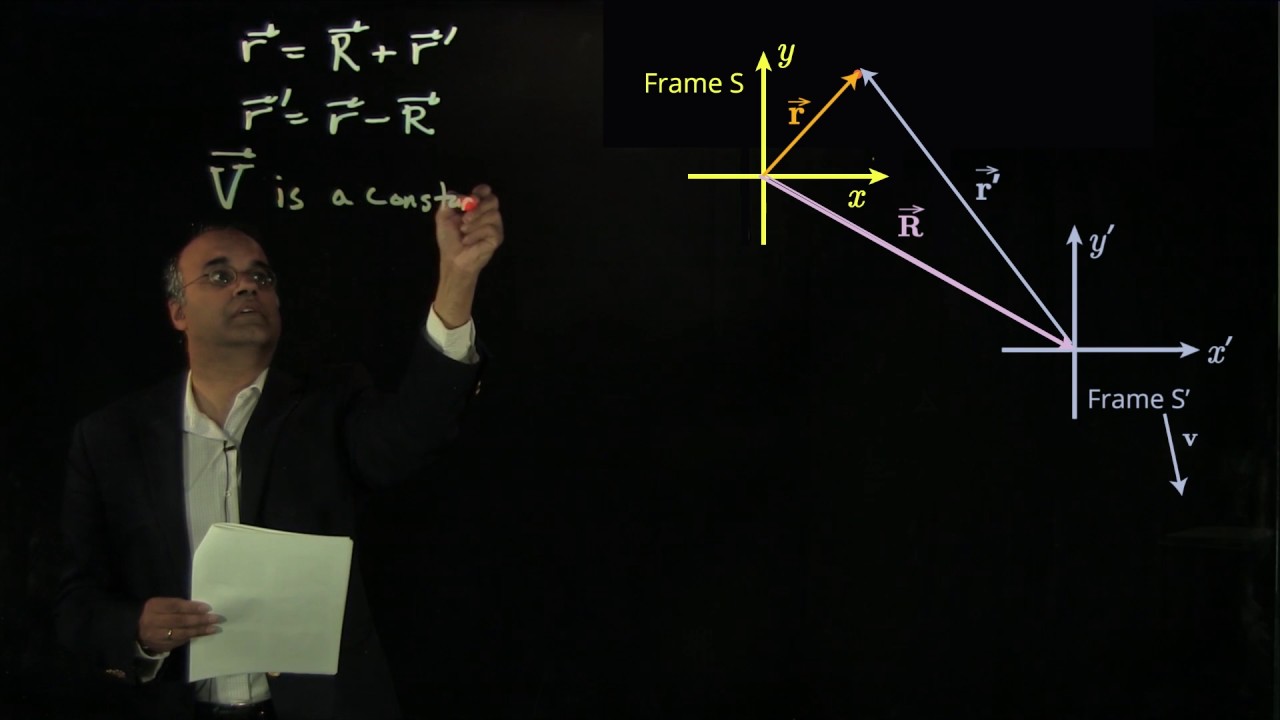
6. Doesn't this equation for the r vector ( r = R + r' ) assume that the second reference frame S' is merely a translation of S? In other words, if S' is rotated with respect to S, ( r ) cannot be equal to ( R + r' ). ( r' ) would then need to be multiplied by the rotation matrix ( call it P ) to have it viewed correctly in frame S. I believe the equation should be ( r = R + Pr' ) where P is the identity matrix for S' being a translated version of S.
   I was wondering this because the same issue arises in the Engineering Dynamics lecture series.

7. Best best………explanation.

8. wonderful! <3

9. excellent sir

10. really thank u

11. Thanks MIT.. It's the best explanation of transformation of inertial frame….
    But why this videos have this small like?…

12. I didn't understand the part where it says the a and a' are equal. isn't the r' moving while the r is resting? how come they have the same acceleration?

13. Sir in 4:43 you said that r prime will appear to be in motion because the distance between the observers changes. What if the S prime observer is moving in a circular path?

14. How is he writing on the screen? Thats so cool!

15. MIT is improving the world by providing free education. Meanwhile my school doesn't even give students soft copy of our lecture notes and tutorials and doesn't give access to lecture videos of higher order subjects to everyone

16. Really neat and clear explanation….

17. amazing 😉

18. thank you

19. what does it mean if "the coordinate axes in frame S' are parallel to, but displaced away from the coordinate axes in frame S"? Also, is the object moving from the origin of Frame S to where it is shown in the video?

20. How can an amazing explanation like this get low views. Without any hesitation the best explanation on the topic !!!

Comments are closed.